7.1 Writing Systems
Dinesh Ramoo
We are already familiar with the concept of the phoneme as a basic unit of sound in a language from the second chapter. We often think of a writing system of a language as consisting of letters. However, for our purposes here, we will use the term grapheme to refer to the smallest unit of writing. A grapheme is a letter or combination of letters that represent a phoneme. Just as we use the forward slashes // to indicate phoneme as use the less than and greater than symbols < > to indicate graphemes. For example, the word ‘dog’ has three phonemes <d>, <o> and <g> that correspond to three phonemes. That seems pretty straightforward. Now think of the word ‘ship.’ The <i> and <p> represent two phonemes but the <sh> combine to form a grapheme to represent the voiceless palato-alveolar fricative /ʃ/. This phoneme is different from a grapheme in that different languages use different graphemes to indicate it. For example, Basque <x>, Turkish, Azerbaijani, Romanian <ş>, French <ch>, Shuswap <s>, and German <sch>.
The examples we saw in terms of graphemes will be familiar to English speakers as they are all from alphabets. In alphabets, the basic correspondence for a grapheme is a phoneme. This is not the case for other writing systems. In addition, not all languages have a transparent connection between graphemes and phonemes. Italian and Spanish tend to be transparent while English and French tend not to be so clear in how the graphemes represent phonemes. For example, think of the variations for the grapheme <a> in the words ‘apple,’ ‘father,’ and ‘gate.’ There are also writing systems where graphemes represent not phonemes but syllables, morphemes or even words. As you will see, these variations have implications for psycholinguistic models as most research is done in languages with alphabetic writing systems.
Logography
The earliest writing systems in the world developed from logograms. In this type of writing system, each grapheme represents a word or morpheme. Examples of logographic systems include Chinese characters, Egyptian hieroglyphs, and Sumerian cuneiforms. You can imagine how it would be impractical to have a separate symbol for every word or morpheme. Therefore, these systems take advantage of the rebus principle. For example, in English the word ‘bee’ and ‘leaf’ can be represented with separate pictures as graphemes. However, when it comes to writing ‘belief,’ instead of creating another picture, we could combine the two pictures to for BEE+LEAF which can be sounded out when reading. A modern development of a logographic system would be the use of emojis. However, emojis are not formalized for any language and so cannot act as a writing system on their own.
There are some interesting examples of logographic writing systems in Canada. Examples include the Ojibwe wiigwaasabakoon. These are bark scrolls with symbols now known as Ojibwe hieroglyphs. They have not been deciphered although it is said that some elders still know what they mean (Geniusz, 2009). They are supposed to contain songs and details of religious rituals and medicine. Another example is the Miꞌkmaw hieroglyphic writing system used in the east coast and islands of Canada. These are known as komqwejwi’kasikl, or “sucker-fish writings” as they resemble the tracks left on the mud by sucker fish. It is possible that they evolved from mnemonic symbols that were used to aid in recalling information. As seen in the example in Figure 7.2 from 1880, later missionaries used the system to write prayers while they also destroyed older scrolls that contained information from the Miꞌkmaw religion.

Syllabary
While a logogram represents an entire word or morpheme, a syllabary is a system where a grapheme represents an entire syllable. Typically, syllabaries use a system whereby there are symbols for individual vowels and consonant-vowel combinations. In most syllabaries, phonetically related syllables would not look similar. For example, the grapheme for /pa/ would not look similar to the grapheme for /pi/. Syllabaries are quite natural in that they represent the smallest units of articulation.
Syllabaries are generally used by languages that have relatively simple syllable structures. Examples of syllabaries include the hiragana and katakana syllabaries used for Japanese and Linear B used for Mycenaean Greek. An amazing example of a syllabary being invented is the Cherokee syllabary (Figure 7.3) invented by Sequoyah in the 1810s to 1820s. While the graphemes were borrowed from the symbols seen by Sequoyah in European alphabets, they represent different phonemes and unlike European writing systems, it is a true syllabary. The stories about Sequoyah’s extraordinary achievement is that he attempted to create graphemes for each word. Finding this too difficult, he went on to develop graphemes for each syllable. It was so successful that it led to the Cherokee Nation’s literacy rate in the 1830s surpassed that of European settlers.
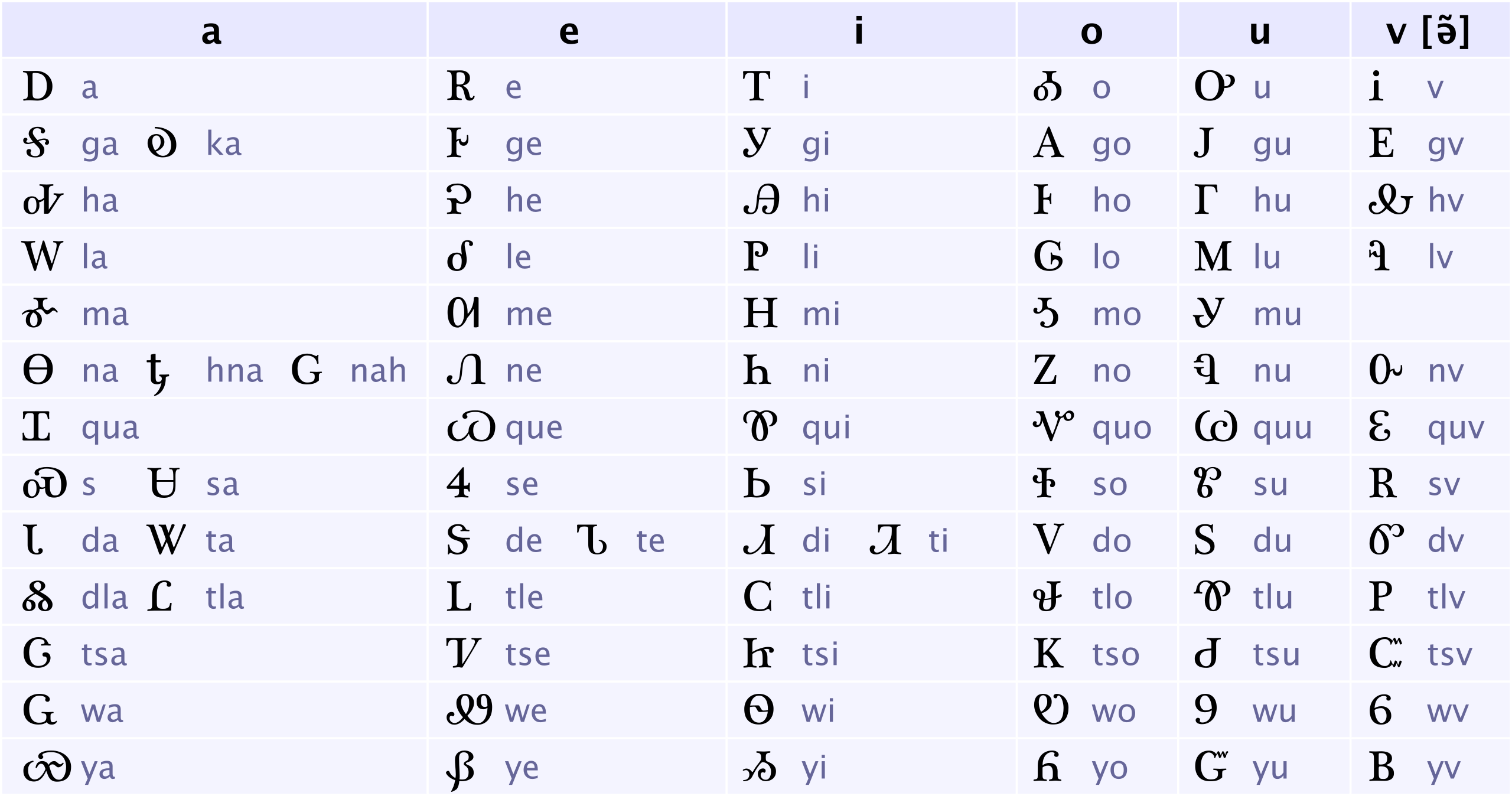
Abjad
Syllabaries seem a very natural way to represent spoken language in writing. They are easily discernable as they represent the smallest unit of articulation. However, some of the earliest systems of writing invented by mankind may appear quite unusual. These are abjads which only have symbols for consonants and not vowels. Why might this be? Try the following exercise.
Living Language
Consider the language that you speak and think of the various dialects that might exist for it. In English, for example, you can think of how people speak in Western parts of North America versus the East Coast. Now compare these against the dialects of English in the United Kingdom, Australia, India, and New Zealand.
Now in imagining how these dialects sound (you can look at some movie clips from various regions), what are the phonemes that are common across them. Do they change a lot in terms of consonants or vowels?
If you went through this exercise, you will realize that vowels tend to be the most varied across dialects of a language. While it may seem natural to us to write vowels down, think of how a person coming up with a system to represent sounds would approach it. As long as you have only a few vowels in your language, you can get the gist of the word by simply writing the consonants. Such systems were used by the people of Ancient Egypt which may have influenced the Phoenicians. The Phoenician abjads lead to Hebrew and Arabic abjads as well as the eventual invention of the alphabet by the Ancient Greeks. As in most writing systems, abjads don’t always remain true to their definition and often employ diacritic marks and some consonant graphemes to represent vowels in some contexts.
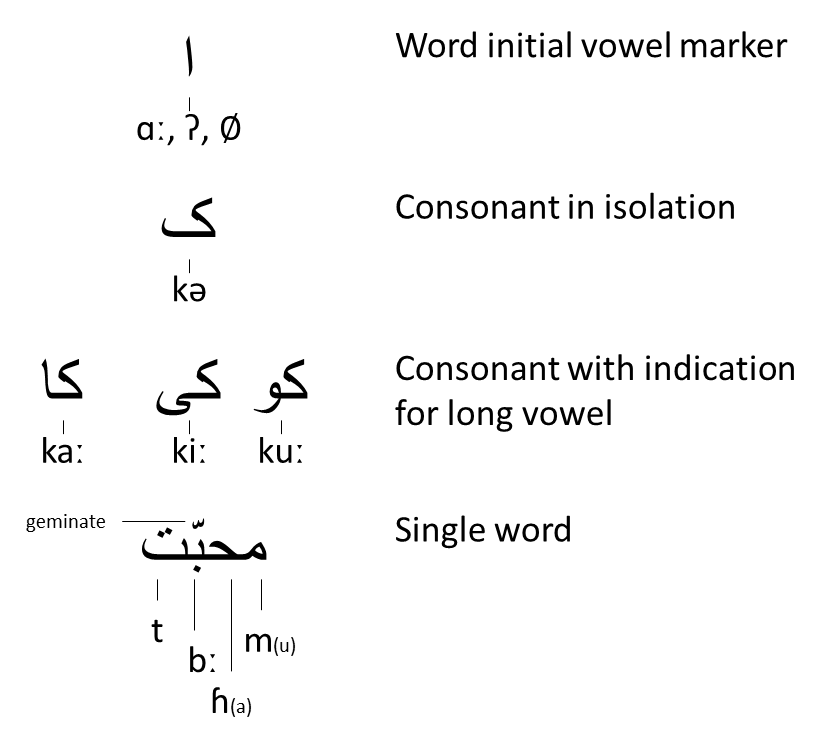
Figure 7.4 gives some examples of the Persian abjad system. Persian has adapted the Arabic abjad to represent its own unique sound inventory. As vowels are quite prominent, Persian employs the aleph symbol from Arabic (originally used to represent a glottal consonant) for vowels. The difference between short and long vowels is indicated by adding a particular consonant for long vowels. Finally, we see a complete word (written right-to-left) with just consonants. Sometimes, diacritics are employed to indicate geminates (overly long consonants). The word itself is a Arabic word (maḥabba) adapted into Persian as /mohæbbæt/ as well as Urdu and Hindi /muhabbat /.
Alphabet
We saw in Chapter 2 that syllables are the smallest units of articulation. Therefore, it is quite natural to represent syllables and words in writing. The alphabet, which represents individual vowels and consonants with separate graphemes is a unique invention of the Ancient Greeks. Taking the abjad system of the Phoenicians, the Greeks adapted it to represent their own language at around the 8th century. As vowels played a more prominent role in Greek, they needed to indicate them with new symbols. The Greek alphabet is the ancestor of all modern European scripts. This is either through its adoption by the Romans for Latin (in the West) and Cyrillic (in the East). Canadian examples of alphabets include Secwepemc (Secwepemctsín), Squamish (Sḵwx̱wú7mesh sníchim), Thompson / Nlaka’pamux (Nłeʔkepmxcín), Okanagan (n̓səl̓xcin̓) and Algonquin (Anicinâbemowin).
Abugida
Unlike an alphabet where the consonant and vowel share equal prominence, an abugida uses segments of consonant-vowel sequences where the consonant is prominent when preceding a vowel. The vowel is usually indicated by secondary notations. This may sound like a syllabary. However, unlike syllabaries, abugida segments can be split into consonants and vowels. In addition, similar segments share visual features.
Most of the writing systems of South Asia, Southeast Asia and Tibet are abugidas. This system is also prevalent in Ethiopian and the Canadian Aboriginal syllabics. Figure 7.5 gives an example of an abugida in the form of the Devanagari script used to write Sanskrit, Hindi, Marathi, and Nepali. Generally, you find separate graphemes for individual vowels and consonants. All consonant grapheme are pronounced with an inherent schwa vowel. If a consonant is followed by a vowel, then it is not written with the primary symbol (as in an alphabet), but with a secondary notation that can appear before, after, under or above the consonant’s grapheme. This is all well and good for simple CV syllables, but what about more complicated syllable structure and syllables that end with a consonant? Various strategies are employed for these scenarios. One is to fuse two consonant graphemes together to form the complex structure (as in the examples for /tr/ and /kj/). We can see that sometimes this fusion results in a new symbol (as in /tr/) or the graphemes for each consonant remain more or less the same (as in /kj/). Another method employed In Hindi is that the final vowel in a word is intuitively deleted based on context. In other languages (for example Sanskrit), there is a special vowel nullifier that is used to indicate that the inherent vowel should not be pronounced.
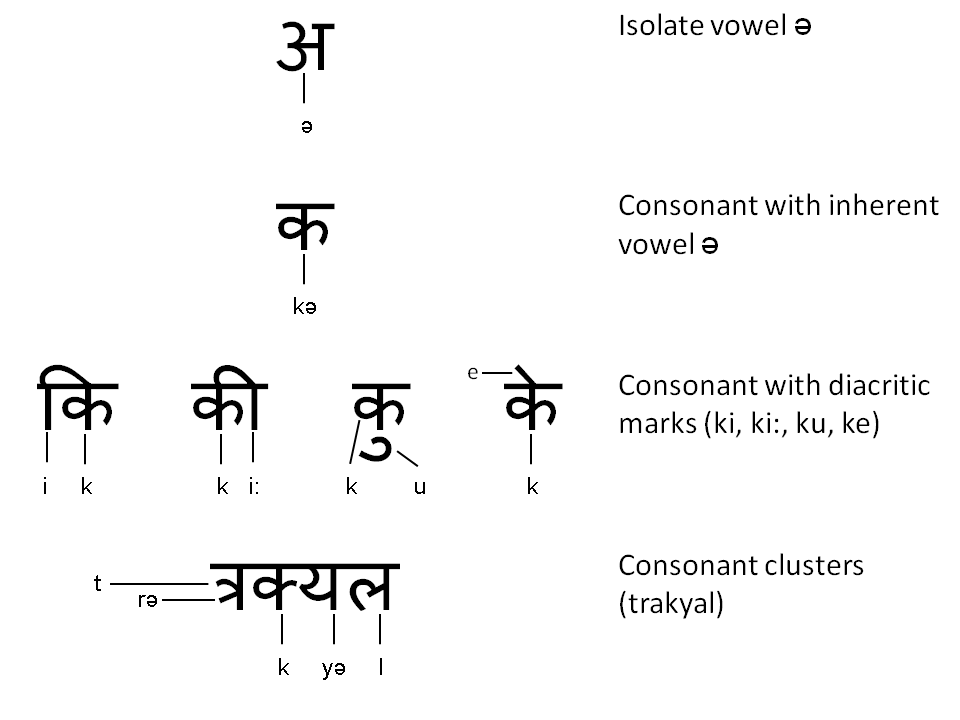
Figure 7.6 gives us a nice comparison between alphabets, syllabaries and abugidas. The alphabet is the Latin script used in English or Secwepemc. Each consonant and vowel have a separate grapheme. However, while in Secwepemc each grapheme represents a phoneme, in English they can represent different phonemes (making the English script less transparent). The syllabary is the Japanese Hiragana equivalents for the Latin graphemes. As you can see, while they represent variations of /k/ with different vowels, they graphemes show no indication of this and are separate symbols. The examples of an abugida are from the Tamil script. Here, we can see the same symbol for /ka/ (in black). However, every other vowel (long /aː/, /i/, /u/, /e/ and /o/) are indicated with secondary vowel notations (in red). This means you need fewer symbols in this writing system as you don’t need a separate symbol for every consonant-vowel combination (as in a syllabary).

An abugida that is prevalent in Canada is a family of writing systems known as Canadian Aboriginal syllabics (see Figure 7.7). Created by James Evans based on his knowledge of Devanagari and shorthand, it is used to write a number of Indigenous Canadian languages. They are used by Cree, Inuktitut and Ojibwe. As seen in Figure 7.7, unlike most abugidas which use secondary graphemes for different vowels, Canadian syllabics are unique in employing the orientation of the grapheme to indicate vowels. If a consonant appears on its own without an inherent vowel, then it is written as a superscript.

Featural Script
We have seen how phonemes can be classified according to their place and manner of articulation as well as voicing. A featural script notates these aspects of phonemes in a consistent manner in graphemes (Sampson, 1990). For example, all labials (phonemes produced with the lips) may have common visual elements in all graphemes that represent them. A writing system developed with just such featural elements is Korean hangul (see Figure 7.8).
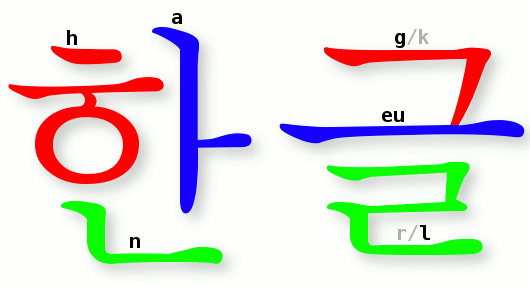
As seen in Figure 7.8, the Korean graphemes are written in blocks arranged in two dimensions. Therefore, words are not written in a linear fashion. Hangul’s featural system is not always evident to its users as the graphemes are used like an alphabetic writing system. Another featural writing system would be Pitman’s shorthand. Here the thickness of the lines indicates featural differences. The fictional script invented by Tolkien for Tengwar also employs featural notations. In it stops look similar to each other with minor variations as do sibilants, fricatives and nasals.
Media Attributions
- Figure 7.2 The Lord’s Prayer in Miꞌkmaw Hieroglyphs is an adapted version of Micmac pater noster by Carl Faulmann that is in the public domain. The original German has been translated into English by Dinesh Ramoo.
- Figure 7.3 Cherokee Syllabary by Sakurambo is in the public domain.
- Figure 7.4 The Persian Writing System by Dinesh Ramoo, the author, is licensed under a CC BY 4.0 licence.
- Figure 7.5 The Devanagari Writing System by Dinesh Ramoo, the author, is licensed under a CC BY 4.0 licence.
- Figure 7.6 Comparing the Latin, Japanese and Tamil Scriptsis by Dinesh Ramoo, the author, is licensed under a CC BY 4.0 licence.
- Figure 7.7 Canadian Aboriginal Syllabics by Timwi is in the public domain.
- Figure 7.8 The word “Hangul”, written in the Korean alphabet by Johannes Barre iGEL (Idea by Immanuel Giel) and is licensed under a CC BY-SA 3.0 Unported license.
The smallest unit of representation in a writing system.
A written character that represents a word or morpheme.
The use of pre-existing pictograms purely for their sound value. For example, bee-leaf to represent the word “belief”.
A writing system where graphemes represent entire syllables.
A writing system where each grapheme stands for a consonant with no or minimal representation of vowels.
A writing system where graphemes exist for consonants and vowels.
A writing system where each grapheme stands for a consonant-vowel syllable. More complicated syllables are represented by combining these graphemes.
A writing system where graphemes represent common elements to represent phonological similarity.

